Сравнив темы учебников 3^eme и 2^de нетрудно заметить не только существенные пересечения в темах, но и исключительную поверхностность: фактически, два года подряд ученики ходят по одному кругу, получая одни и те же несистематизированные представления о физических явлениях. Я уж не говорю о том, что никакой связи с математикой нет и в помине – математика изучается по программе, никак не согласованной с физикой.

Во французской образовательной системе зачастую используется методический прием, при котором одни и те же темы, факты и явления обсуждаются «по спирали»: сначала дается общее представление об изучаемом предмете, затем через год тот же предмет обсуждается с большей подробностью и с несколько других позиций, и т.д. Мне трудно сказать, насколько подобный методический прием пригоден в гуманитарных областях, таких, как история, литература, обществоведение, но в изучать физику таким образом никак нельзя. Одна из основных проблем заключается в том, что такое «спиральное» изучение негуманитарных предметов нарушает естественный синергизм разных областей знания, в частности, физики и математики: «спираль» физики и «спираль» математики имеют разные периоды и не накладываются друг на друга.

2. Как объяснить физику и математику «нефизматшкольникам», чтобы было интересно? Примеры из каникулярной программы

Во Франции существуют заочные физматшколы, рассчитанные на детей, которые интересуются естественными науками, в первую очередь, математикой и физикой. Для детей, углубленно занимающихся физикой, стандартный школьный учебник физики нужен лишь в качестве «реперной точки» для того, чтобы знать, какие именно темы могут войти в экзаменационную программу. В качестве учебного пособия он пригоден не более, чем меню в китайском ресторане для изучения китайского языка. В то же время, «нефизматшкольники» во Франции оказались в сложной «периферийной» ситуации: ими никто специально не занимается, хотя их большинство. То, что для «физматшкольника» представляется очевидным и естественным, у «нефизматшкольника» вызывает удивление, и тогда преподавателю надо искать обходные пути, не полагаясь на учебник. Иногда достаточно просто отойти немного в сторону от традиционного изложения, принятого в школьной программе, и ориентироваться не на абстрактное мышление и аксиоматику, а на чувственное восприятие и повседневный жизненный опыт.

Приведу несколько конкретных примеров (с иллюстрациями) того как мы пытались объединить физику и математику, геометрию, оптику и механическое движение, апеллируя к простым наглядным построениям.

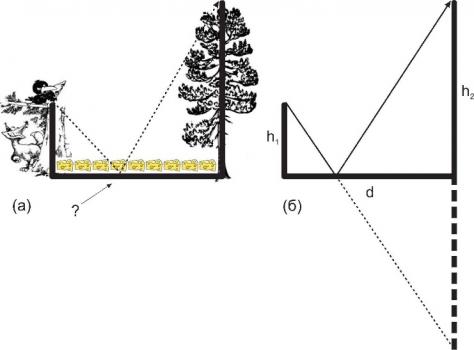
1. Мы начали с такой простой задачи. На вершине дерева высоты h1 сидит ленивая ворона и хочет перелететь на вершину другого дерева высоты h2, стоящего на расстоянии d от первого. Между деревьями разбросан сыр и ленивая ворона хочет схватить такой (один) кусочек сыра, чтобы расстояние, которое она пролетела с одного дерева на другое, было бы минимальным. Вопрос заключается в том, чтобы указать какой именно кусочек сыра схватит ворона – см рис.1а.
Ответ: кратчайшее расстояние между деревьями – прямая, поэтому одно из деревьев нужно зеркально отразить относительно земли и провести прямую от вершины одного дерева до образа другого как схематично показано на рисунке 1б

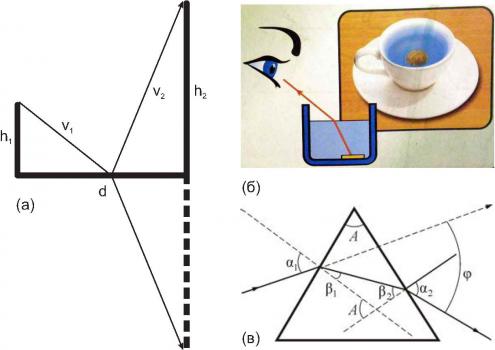
Давайте теперь определим положение кусочка сыра, если прожорливая ворона хочет минимизировать время общего полета, при этом она летит до кусочка сыра со скоростью v₁, а схватив его становится тяжелее и от кусочка до своей цели (другого дерева) летит со скоростью v2 (v₂ < v₁) – см рисунок 2а.

Я думал, что после того, как ребята решат задачу про прожорливую ленивую ворону, я им расскажу, что именно так устроено преломление лучей в геометрической оптике при прохождении света из менее оптически плотной в более плотную среду, и вообще, вся физика основана на принципе минимума действия, которое в данном случае есть время перелета с дерева на дерево… Но не получилось. Оказалось, что использовать для решения задачи производную (чтобы определить минимум некоторой функции) им не пришло в голову, потому что производная живет в курсе математики, а мы пытались решать физическую задачу. В результате пришлось рассказывать о том, что такое функция и экстремальные значения - первая и вторая производные - и что это то же самое, что скорость и ускорение для механического движения…

Я воспользуюсь случаем и все-таки, расскажу про то, что случилось с ленивой прожорливой вороной, поскольку несмотря на простоту, эта задача отражает фундаментальный физический принцип - так называемый принцип минимума действия, лежащий в основе как классической, так и квантовой физики. В геометрической оптике этот принцип известен как принцип Ферма, в соответствии с которым лучи распространяются так, что время, пройденное светом от начальной до конечной точки, должно быть минимальным. В частности, задача о ленивой вороне позволяет в деталях понять хорошо известный «опыт о невидимой монете» (см. рис.2б). Монета лежит на дне чашки, и если смотреть под некоторым углом, то края чашки закрывают монету, и она не видна. Однако, если в чашку налить воду, то мы увидим монету. Происходит это именно из-за того, что лучи преломляются при прохождении света из менее оптически плотной в более плотную среду. По этой же причине призма раскладывает свет на составляющие (см. рис.2в). Каждый цвет отвечает определенной частоте и имеет свою «групповую скорость» распространения в среде. Чем меньше скорость, тем сильнее отклонения луча в призме.

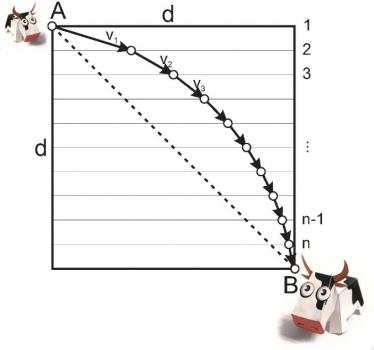
2. Продолжением этой истории стала задача о ленивой корове на поле. Пусть есть квадратное поле размера d x d, которое разделено на n горизонтальных грядок, на которых растет сочная трава (а между ними ничего не растет). В углу A (см. рисунок 3) стоит ленивая корова, которая хочет пройти по полю в точку B, съедая по дороге траву с грядок. Начальная скорость коровы v₁. Каждый раз, когда корова съедает траву с грядки, корова подрастает, ей становится труднее идти и ее скорость уменьшается на величину d. Таким образом, после первой грядки скорость коровы v₂ = v₁-d, после второй грядки v₃ = v₂-d = v₁-2d и т.д., до тех пор, пока корова не достигнет точки B, где остановится, т.е. ее скорость станет равной нулю: v_n+1 = 0 (для этого должно быть d = v₁/n). Нужно определить форму пути, по которому шла корова, если грядок очень много (n >> 1), и если бы корова хотела минимизировать время своей прогулки.
Ответ довольно забавный: корова должна идти не по прямой, а по дуге окружности. Это наводит на размышления о том, что в зависимости от свойств пространства (т.е. в зависимости от того, по какому правилу идет корова по грядкам), самый короткий путь (прямая) не всегда самый быстрый. Данную задачу можно использовать в качестве наивной иллюстрации того, как метрика пространства искривляет лучи света.

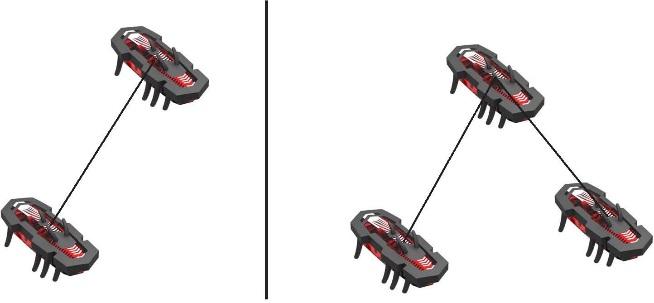
3. Одно занятие во время летней школы мы посвятили обсуждению возможности создания простых устройств, которые могут направленно перемещаться из-за наличия внутренних колебаний и трения. Я собирался купить в магазине игрушек «тараканов» hexbug-nano, которые выглядят как на рисунке 4 (продаются также в Amazon.com). План был следующий:

- во-первых, я хотел предложить обсудить, как именно они движутся, и рассказать о том, что подобным образом устроены простейшие молекулярные машины в биологии;

- во-вторых, предполагалось связать двух, а затем, трех тараканов нитью, и исследовать характер их движения. Гипотеза заключалась в том, что два связанных между собой таракана будут вращаться вокруг общего центра, который будет двигаться поступательно, а движение трех связанных тараканов уже нельзя будет разложить на поступательное и вращательное движения, и будет непредсказуемым.

К сожалению, в магазине тараканов не оказалось и пришлось делать насекомое из подсобных материалов: две батарейки AA, скрепка, карманный вентилятор за 2 евро, из которого был вынут мотор, пробка от Côte du Rhône, аптечная резинка, клей super glue и 4 зубочистки. В результа-те получилось насекомое, изображенное на рисунке 5. Кусочек пробки был надет асимметрично на ротор мотора, поэтому при вращении вся конструкция сильно виб-рировала, а согнутые под углом ноги создавали направленную силу из-за асимметрии трения. Наших усилий хватило только на одну такую машину, поэтому вопрос о коллективном движении насекомых пока остался открытым. Но наше насекомое вполне уверенно ползало по гладкому столу. Попытка запустить его за ужином в приличном ресторане Ниццы была пресечена организаторами школы. Надеюсь, в дальнейшем мы сможем освободиться от навязчивых административных регламентаций для наших научных экспериментов:)